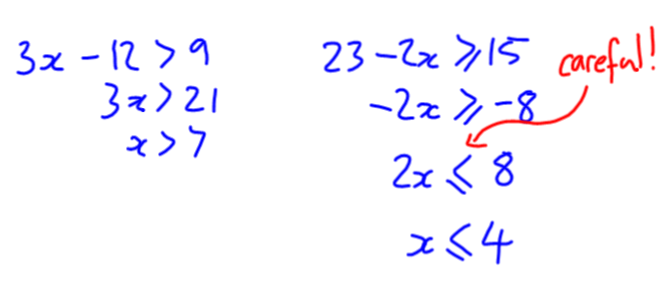Semester 2 has started, which means the Computer Science elective I was teaching has ended. The good news is, I’ve taken over Year 10 Maths, which means my teaching load is more maths than it’s ever been before. I haven’t taught Year 10 for a couple of years now, and I’ve changed the way I teach a lot even in the last 12 months. Luckily, I had this same class last year so they’re pretty used to how I do things.
The first unit I’m teaching is Linear Relationships:
Most recently we’ve been working on LR2, linear inequalities. If these are taught as a totally procedural matter, it’s a fairly easy topic: solve them the same way as equations, just being careful with the direction of <, >, ≤ or ≥ if dealing with negatives. But as I always tell my students, I believe our aim is not to ‘get the right answer’, but to understand.
In particular, I want my students to understand that there is not just a single solution, but a whole set of solutions. I want them to understand that when we write a statement such as x ≥ -2, we are describing a rule by which some values are included and some are not. So I started the lesson by looking at a couple of examples:
A little is lost when seeing this as a static IWB page, as opposed to the notes that developed through class discussion. Importantly, all the possible solutions were provided by students. I was really pleased with their suggestions, in that they illustrated some important points about inequalities. For example, 4.999999999 is indeed less than five, as are all negative numbers. And I liked the suggestion of 6000893, pointing out that there isn’t an upper limit for x ≥ -2. And I impressed the student by hearing and remembering the number he called out :).
Next I gave an example of an inequality to solve. Rather than getting the class to solve it as an equation, I had them each make a list of five values that would be included in the solution, and five that are not. We then shared some of these as a class:
What this allowed us to do was find the solution to the equation by understanding what the equation described. It’s important as a maths teacher to ensure students know why they do things they do. When students solve equations, they shouldn’t following a list a pre-described steps to get ‘the answer’. They should be trying to answer the question, “What value makes this statement true?”
We also looked at 23 – 2x ≥ 15, and found that our solution doesn’t necessarily have the same direction as the inequality. My students quickly identified the negative in front of the x as the culprit. As one student pointed out, you need to make x smaller if you want 23 – 2x to get larger.
So, the class found two important pieces of information are needed to find the solution to an inequality:
- What is the boundary between the solutions that are included and the solutions that are not?
- Which direction do those solutions go in?
And how do we find this information? Using algebra, of course!
It’s at this point that I believe procedure becomes useful: after that understanding has been built. I’m increasingly finding that a good way to get students to follow a process I give them is to use a less efficient method they understand to do the same thing first. Students could solve inequalities by finding test cases each time, but they find solving them algebraically is a much quicker process. They look for shortcuts to make their work easier. Just like mathematicians do.