Posted on

Homemade Algebra Tiles

I’ve been lacking in the algebra tile department lately. They aren’t the cheapest things to buy, so I decided to make my own.

My very own homemade algebra tiles

They actually turned out a lot better than I expected. As you can see, they’re double sided for negatives, and include the variables x and y. I’m not sure how long they’ll survive once they get into the hands of students; they’re laminated, but the two layers of paper are only held together by glue stick. For now, though, they seem pretty sturdy.

Lots of lovely tiles in bags

While there are probably other algebra tile templates online, I made my own, which you can download here:

Here’s how to put them together:

  1. You will need:
    • Printer.
    • Various colors of paper.
    • Red cardstock. Or just paper. I used cardstock because that’s what I had, but I think it helped make the tiles a lot sturdier.
    • Glue. I used a glue stick, but there may be better options. I want to try a spray adhesive next time.
    • Laminator and laminating sheets.
    • Scissors and/or other paper cutting device.
  2. Print the positive sides (odd numbered pages) on the colored paper. Make sure every page is printing using the same scale. (I just printed at “actual size” to make it easier.)
  3. Print the negative sides (even numbered pages) on the red cardstock.
  4. Cut around the dotted border on the -1 page. (Page 2).
  5. On the +1 page (page 1), use a pencil to mark where the outside corners are on the back of the paper. Hold the paper up to a light if it helps.
  6. This is the tricky bit: Glue the -1 page to the +1 page, back to back. Be very careful to glue the entire surface, or any gaps will become tiles that have nothing holding them together. Use the pencil marks to line the pages up.
  7. Repeat for all the other pages.
  8. Laminate each set of tiles.
  9. Carefully cut the tiles apart.

Was this the best use of my time a week before school goes back? Almost certainly not. But doing something crafty to prepare for school has helped get me more enthused about the upcoming year, and more motivated to get the important things done. Maybe a small project like this is what you need, too.

Actually, the main impetus for making these tiles is the presentation I’m giving at the #NEOKMath Teacher Conference in a couple of days (Thursday, August 5). I’m talking about methods to familiarize students with the distributive property, which includes using algebra tiles. If you’re reading this the day I post it, and you live in north east Oklahoma or nearby, it’s not to late to sign up to attend. And it’s free. I won’t even be offended if you skip my session to hear someone else.

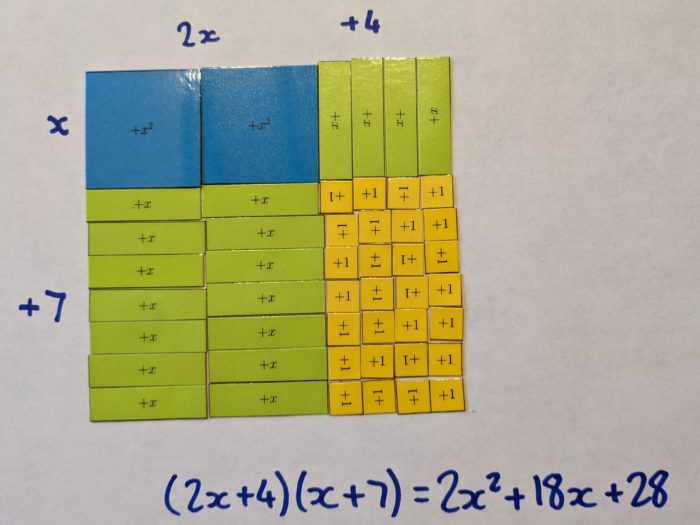
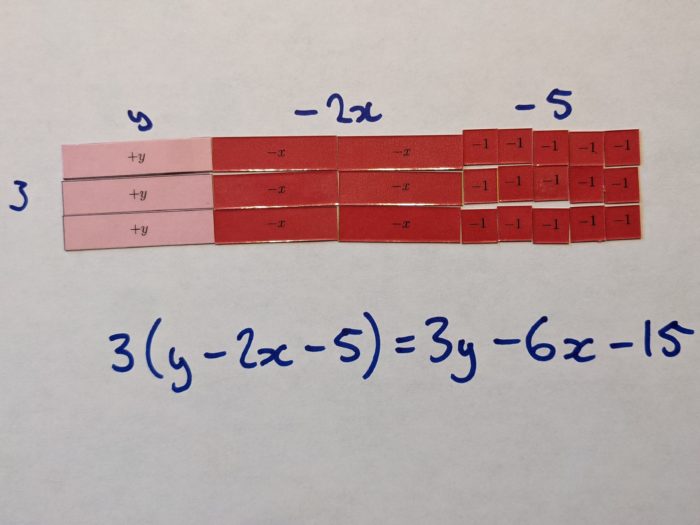
Here’s a couple of examples I made for my presentation, using these tiles:

 
Posted on

Algebra 2 Class Notes v 0.3

Here’s the next version of my notes. If you’ve missed this so far, I’m writing a complete set of fill-in-the-blank notes for Algebra 2, specifically with the Oklahoma Academic Standards in mind. See my post sharing the first draft of the notes for my reasons for doing this.

There’s a lot of small fixes here, with things that could be written clearer, some additional examples, and, sadly, a lot of typos and other mistakes. The most substantial edits were to section 8.4, on natural exponents and logarithms. I’ve always been dissatisfied with the way the value of the constant e is justified in classes which precede calculus. I’m hoping that this explanation will satisfy students by alluding to the calculus, without teaching it explicitly.

Downloads are available here:

 
Posted on

Algebra 2 Class Notes v 0.2

UPDATE: version 0.3 of these notes are out now.

In my last post, I made available notes for the entire year of Algebra 2, following the Oklahoma standards. I mentioned that the notes are a work in progress. Hopefully in time for the new school year for most, here is an updated version.

Changes focus on the first six chapters, which should get anyone following the notes in order through the fall semester. I aim to have version 0.3, which will focus on fixes to the remaining chapters, done by Christmas.

Changes include:

  • Fixes to lots of errors and typos, both in the text and in the worked examples.
  • A number of paragraphs rewritten to be clearer.
  • A handful of additional examples.
  • Additional space for select examples.
  • Additional diagrams to explain concepts, including the picture below.

As before, there is a set of blank notes for students, and a set of the notes with all the blanks and examples completed. These notes remain free to use for teachers to distribute to their students in their own classes.

Download here:

 
Posted on

Algebra 2 Class Notes v. 0.1

UPDATE: version 0.3 of these notes are out now.

I’ve been working on a big project over summer: a set of student notes with fully worked examples for an entire year of Algebra 2.

You might be wondering why I did this. I’m not even teaching High School currently, as I’m taking a couple of years to attend grad school. While I’m doing some teaching, it’s been as a TA for Calculus 1, certainly not for Algebra 2. Even so, I’ve still spent a lot of time thinking about Algebra 2 curriculum over the past year, and had a lot of conversations about it with Sarah, as she is has been teaching Algebra 2 since last August. It turns out, even after taking some time away, my passion is still for high school math.

These are the ideas I’ve had for the function of these notes:

  • They’re aiming to meet the Oklahoma Academic Standards, though in places they step back to strengthen the conceptual foundation, and in others they go beyond the standards. Eventually I’ll produce an alignment document to explain all the links.
  • This is not a complete curriculum, but I see it functioning as a “skeleton” on which a complete curriculum could be built.
  • The notes focus almost purely on the mathematics, not on “real world” applications (with a few exceptions in statistics topics). This is not because these are unimportant; on the contrary, they are vital. But I believe these are better addressed using methods other that pre-prepared notes.
  • The intent is that the notes would be hole-punched and kept in a binder. This means if a teacher doesn’t like how I’ve done something, they can change it. Remove the parts you don’t like. If you don’t think there are enough examples, add more.
  • Teachers can incorporate the notes and examples as they wish into their lessons. While textbooks give they answers to examples away from the start, with fill-in-the-blanks, the teacher can choose at what point in the class discussion they make the correct answers known.

You might remember that I was working on a book of Algebra 2 practice questions. That’s still ongoing, but it’s been overtaken somewhat by these notes. But that’s okay, because I see these as two aspects of the same long-term project. Having the notes planned out should make planning questions a lot easier.

If all of this sounds good, here’s the great news: I’m going release the notes as I work on them. And while they’re still just a first draft at this point, that first draft is entirely done, and hopefully in a usable form for the upcoming school year.

Download them here:

 
Posted on

Quadratic Vertex Form Card Sort

Over the weekend, I needed a break from working on grad school assignments. At the same time, Sarah needed a card sort on the vertex form of quadratic functions. Being the nice husband I am, I thought I’d help. Being the nerd that I am, I did it in LaTeX.

This took a bit longer that I’d expected to create. I’ve a little experience creating graphs, so they weren’t too bad, but tables in LaTeX can be a little fiddly to get right. I also wouldn’t claim that took much thought went into choosing which functions to use. But, I’m pretty happy with the result.

You can download the files here. Included is the shuffled set of cards (pictured above), the cards sorted into the correct order, and a zip file of the original .tex files in case you want to modify them at all.

Edit (Oct 23): There were a couple of mistakes in the original version, it has been fixed now.