Sieve of Eratosthenes worksheet

To start by stating the obvious: I have not blogged enough this year. As in, my last post was before the school year had even started. I could make excuses (which would basically consist of ‘way too busy’, ‘not enough time’, ‘seriously, I’m crazy busy’), but I know I’m a better teacher when I blog. I know the constant process of self reflection is good for my ability to be self-critical.

Now that I’m starting my favourite topic of all time with Year 7, Primes and Indices, I thought this was a good chance to get back into this blogging thing. As my girlfriend reminded me the other day, I’ve been known to write ‘#primenumbersaremyjam’ in messages before. Number Theory was my favourite uni subject by far. And, I guess you noticed the title of this blog. I also may have gone through the proof that there are an infinite number of primes with my Year 12s today (which has very little to do with the differentiation we were supposed to be doing).

So I get just a little bit excited when I get to teach this. 😉

So, the Sieve of Eratosthenes, aka ‘that thing where you cross off a bunch of numbers to find the prime numbers’. If you’re not familiar with it, the process is this:

• Ignore 1, because it is neither prime or composite. 🙂
• Select the first number, which is of course 2. We’ve found our first prime!
• Eliminate all the multiples of 2 (except 2 itself), as these are not prime.
• Select the next number that is left, which should be 3. This is also prime.
• Eliminate all the multiples of 3.
• Select the next prime number, which is 5. (4 was eliminated by 2). Eliminate its multiples.
• Continue this process to find the rest of the prime numbers.

I googled for a worksheet for this (or really any number grid would’ve done), but I wasn’t really happy with what I found. Most number grids seem to go up to 100 or 120, but I wanted to go to 150. Mostly so I could include 121, and make it necessary to cross off the multiples of 11 (there are smaller multiples of 11, of course, but they’re all eliminated by the smaller primes). The next step, then, was to throw together my own worksheet, which looks a little (or exactly) like this:

Some people may have decided that ‘Finding Prime Numbers’ would make a better, less confusing title for students, but I disagree. I think we need to expose our kids to the accepted terminology, so they can communicate in correct mathematical language. We just need to teach them what the terms mean, which is our job, by the way. I get rather annoyed when I see students being told they’re studying ‘chance’, say. Call it ‘probability’. Because that’s what it’s called. #pettyrantover

I decided that this time I would be really precise with how I wanted students to mark off their sheet:

• Colour in each prime completely using a different colour. (After 11, I let them start using a single colour, because they would have run out.)
• When eliminating composites, draw a single line through each multiple in the same colour as the prime number. If a number has multiple prime factors, it gets multiple lines through it.

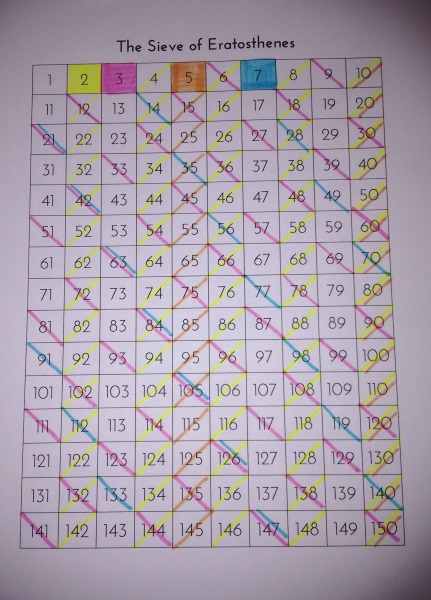
My partially completed sheet. Unfortunately the rest of my awesome highlighters are at school, and I am at home. But it should give you the idea.

This, for one thing, made the sheets a lot neater. But it also made it easier for kids to notice patterns. Patterns which they kept showing me completely un-prompted. I had students not only tell me that the multiples of 11 make a diagonal line, but they explained why that happens. #mathsteacherjoy

Another moment of joy came when I saw students write down their reasons that 2 is prime, using the definition of prime numbers. 🙂

Downloads for this worksheet are here:

• PDF: The Sieve of Eratosthenes.pdf
• Editable Word document: The Sieve of Eratosthenes.docx
  (You’ll need the font ‘Josefin Sans’ if you don’t want it to look weird.)